Decentralized Diffusion Models

Train diffusion models across many GPU clusters without networking bottlenecks.

Some samples from our largest Decentralized Diffusion Model, pretrained with just eight independent GPU nodes in less than a week.

State of the art image and video diffusion models train on thousands of GPUs. They distribute computation then synchronize gradients across them at each optimization step. This incurs a massive networking load, which means that training clusters must live in centralized facilities with specialized networking hardware and enormous power delivery systems.

This is cost-prohibitive. Academic labs can’t build specialized clusters with custom networking fabrics. Even large companies struggle as they hit fundamental limits on power delivery and networking bandwidth when scaling to many thousands of GPUs. In both cases, networking is the critical bottleneck: training clusters need constant, high-bandwidth communication throughout the entire system. A segmented network load where independent clusters communicate internally but not among each other makes it possible to use compute where it’s available, whether in different datacenters or across the internet.

Decentralized Diffusion Models (DDMs) tackle this problem. Our new method trains a series of expert diffusion models, each in communication isolation from one another. This means we can train them in different locations and on different hardware. At inference time, they ensemble through a lightweight learned router. We show that this ensemble collectively optimizes the same objective as a single diffusion model trained over the whole dataset (a monolithic model). It even outperforms monolithic diffusion models FLOP-for-FLOP, leveraging sparse computation at train and test time. Crucially, DDMs scale gracefully to billions of parameters and produce great results with reduced pretraining budgets. See some results below from a model pretrained with just eight independent GPU nodes in less than a week.

In this post, we present a simple, geometrically intuitive view on diffusion and flow models from which Decentralized Diffusion Models arrive naturally. We also highlight their compromise-free performance and implications for training hardware. DDMs make possible simpler training systems that produce better models.

Simple Intuitions for Diffusion and Flow Models

Diffusion models can be geometrically intuitive. We aim to show some of these ideas in this post.

Diffusion models and rectified flows can be seen as special cases of flow matching, so we use the FM framework to explain DDMs. Most perspectives on diffusion models and flow matching focus on the forward corruption process and the paths it samples for each training example. Let’s instead focus on the training/regression target of these models: the marginal flow. They all minimize the difference between their predictions and the marginal flow.

The marginal flow, $u_t(x_t)$, represents a vector field at each timestep that transports from $x_t$, a noisy variable, to the data distribution ($x_t$ at $t=0$). When we train with flow matching, we regress the marginal flow into a model (e.g., a Diffusion Transformer) that can sample the data distribution. The marginal flow in its analytical form is an expectation over $x_0$ data samples. That is, the marginal flow is linear. For any given $x_t$, it points toward the data distribution from $x_t$. In high dimensions with many data points, this is intractable to compute. Instead, diffusion models compress this complex system into a neural network through flow matching.

Let’s rewrite the marginal flow as a sum over a discrete dataset for clarity. $q(x_0)$ is a constant now. It’s now easy to see that the marginal flow is just a weighted average of the paths from $x_t$ to each data point, $u_t(x_t|x_0)$. Each path $u_t(x_t|x_0)$ is called a “conditional flow,” pointing from $x_t$ to a specific data sample $x_0$. We marginalize over these conditional flows to get the marginal flow. The weights of each path are determined by the normalized probability of drawing $x_t$ from a Gaussian centered at each $x_0$ sample, $p_t(x_t|x_0)$.

Sampling from the marginal flow is simple. At the maximum timestep $t=1$, $x_t$ is drawn from the Gaussian distribution. Then, we can transport $x_t$ to a sample from the data distribution by integrating the marginal flow backwards in time. This just means taking steps in the direction of the marginal flow at progressively decreasing timesteps. In other words, just keep taking small steps toward a weighted average of the data points and you’ll converge to a sample. Machine learning is effective at learning these weighted averages through reconstruction objectives. The meat of this interpretation is not new—it’s highly related to score matching, SDEs and Tweedie’s formula. These connections are covered much more thoroughly in this blog post.

We highlight a new interpretation because it compactly motivates DDMs. Our interpretation is maybe the simplest way to understand the main ideas of this family of models. It also shows that these models can be geometrically intuitive. Since we can compute the marginal flow analytically over small datasets, we can visualize it interactively in 2D. We made the plot below to show how the components of flow-based models interact.

In the following live plot:

Data points ($x_0$ samples) are dark blue.
Each path/conditional flow, $u_t(x_t|x_0)$, is drawn in turquoise and its opacity represents its weight (“path weight” above).
The noisy latent ($x_t$) is red. Drag it around to see how each training example affects the denoising path from $x_t$ to the data distribution at different values of $t$.
The red dotted line shows the predicted denoising path, AKA the marginal flow, evaluated analytically that points from $x_t$ to the weighted average of the data, $\hat{x}_0$.
The slider below simulates the denoising (decreasing $t$) and the noising (increasing $t$) processes.

Since the marginal flow is defined at each timestep, the slider updates the timestep t. $x_t$ will be transported accordingly by Euler integrating the marginal flow forward or backward in time. The data points will also change in magnitude according to a simple linear schedule, $(1-t)*x_0$, the mean of the Gaussians that define $p_t(x_t|x_0)$. At low timesteps, the path weights are much peakier and $x_t$ will be drawn to its nearest neighbor. Play around, this simulates a “perfectly overfit” diffusion model. For example, try dragging $x_t$ around the points with the slider set to $t=0.10$.

This interpretation sets up Decentralized Diffusion Models very naturally. The marginal flow is a linear system, and linear systems are associative. DDMs exploit this associativity to simplify training systems and improve downstream performance.

Decentralized Diffusion Models

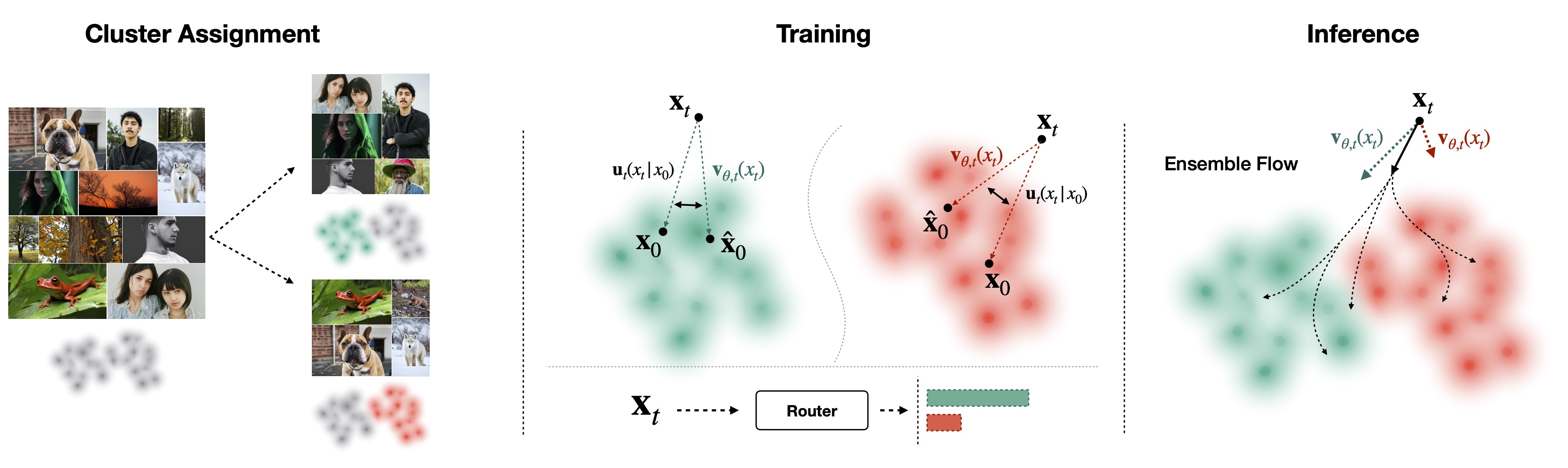
Decentralized Diffusion Models leverage the associative property of the marginal flow to split training into many independent sub-training jobs focused on producing “flow experts” that each model a subset of the data. These have no data dependencies to each other, so they can be trained wherever compute is available.

We partition the data into K disjoint clusters ${S_1, S_2, \ldots, S_K}$, and each expert trains on an assigned subset $(x_0 \in S_i)$. Since the marginal flow is a linear combination over data points, we can apply the associative property within each of these data clusters. We therefore rewrite the global marginal flow as a weighted combination of marginal flows over each data partition.

We train a separate diffusion model over each individual data cluster. This is standard flow matching training, so we can reuse popular architectures, hyperparameters and codebases. By adaptively averaging each model’s prediction at test-time, we sample from the entire distribution and optimize the global flow matching objective. We must learn a router to predict the adaptive weights of each expert model at test-time, which we train with a classification objective over the data clusters. We discuss this more thoroughly in the paper.

We can visualize the component flows of a Decentralized Diffusion Model in the plot below. By ensembling them at test-time, we recover the global marginal flow. Drag the black $x_t$ circle to see the denoising predictions for each expert model (blue and red). Slide the time slider to see how the ensembled denoising predictions update the particle $x_t$.

The figure below outlines the data preprocessing, training and inference stages of Decentralized Diffusion Models:

Decentralized Diffusion Models follow a three-step training process. We first cluster the dataset using an off-the-shelf representation model (DINOv2). We train a diffusion model over each of these clusters and a router that associates any input $x_t$ with its most likely clusters. At test-time, given a noisy sample, each expert (in red and green) predict their own flows, which combine linearly via the weights predicted by the router. The combined flow samples the entire distribution and is illustrated on the right.

Why DDMs?

These are all cute observations, but why does it matter?

Associativity is the key enabler behind many distributed computing algorithms including parallel scans and MapReduce. Decentralized Diffusion Models use the associative property to split diffusion training into many sub-training jobs that proceed independently, with no cross-communication. This means each training job can be assigned to a different cluster in a different location and with different hardware. For example, we train a text-to-image diffusion model on eight independent nodes (8 GPUs each) for around a week. These nodes are readily available to rent from cloud providers, whereas eight nodes with high-bandwidth interconnect must be co-located in one datacenter and are much harder (and more expensive!) to procure.

Some nice generated images from the eight-node training run.

What’s the performance hit from this added convenience? There is none. In fact, Decentralized Diffusion Models outperform non-decentralized diffusion models FLOP-for-FLOP.

Comparing DDMs and standard monolithic diffusion models. FLOP-for-FLOP, decentralized diffusion models outperform monolith diffusion models on both ImageNet and LAION Aesthetics.

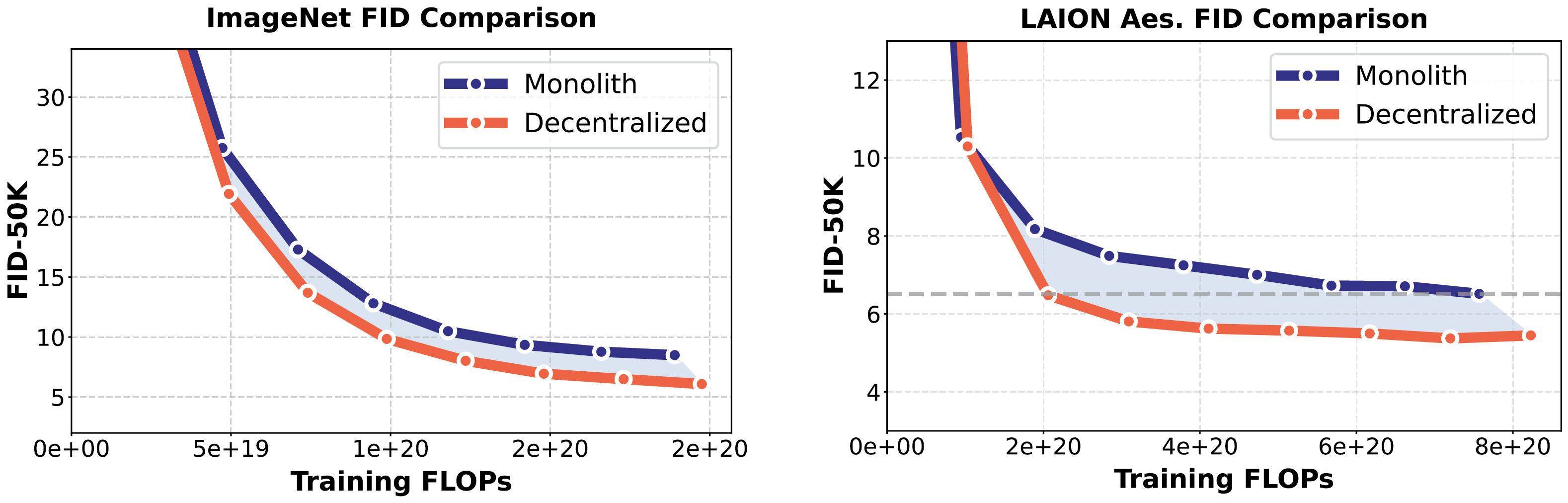
By selecting only the most relevant expert model per step at test-time, the ensemble instantiates a sparse model. We can view this as activating only a subset of the parameters of a much larger model, resulting in better performance at the same computational cost. This is also the driving insight in Mixture-of-Experts. We use the same architectures, datasets and training hyperparameters between monoliths and DDMs in all our evaluations, and we account for the additional cost of training the router (~4%). Serving a sparse model can be inconvenient with less sophisticated infrastructure, so we also demonstrate that we can efficiently distill DDMs into monolith models in the paper.

Decentralized diffusion models scale gracefully to billions of parameters. We find that increasing expert model capacity and training compute predictably improves performance.

Decentralized Diffusion Models also scale gracefully. We see consistent improvements on evaluations as model size and compute capacity increased. Please see the paper for more detailed analysis of DDMs and how they compare to standard diffusion training.

Simple Implementation

Decentralized Diffusion Models integrate seamlessly into existing diffusion training environments. In implementation, DDMs involve clustering a dataset then training a standard diffusion model on each cluster. This means nearly everything from existing diffusion infrastructure can be reused. This includes training code, dataloading pipelines, systems optimizations, noise schedules and architectures.

To highlight this, we’ve included a simple code example of how to modify a diffusion training loop to be a DDM in PyTorch.

# Inside a standard diffusion training loop:
x = next(dataset)
t = torch.randint(0, T, (1,))
noise = torch.randn_like(x)
x_t = forward_diffuse(x, t, noise)

pred = model(x_t, t)
x_0_pred = reverse_diffuse(x_t, t, noise, pred)
loss = F.mse_loss(x_0_pred, x)
loss.backward()
optimizer.step()

To make this a DDM, we first cluster the dataset using a representation model. We used DINOv2 and this codebase to run k-means clustering on a large dataset. We then train a diffusion model over each cluster. This is completely unchanged from standard diffusion training like above.

The last step is to train a router that predicts the weights of each expert model at test-time. This reduces to a classification objective over the data clusters.

# Inside a DDM router training loop:
x, cluster_idx = next(dataset)
t = torch.randint(0, T, (1,))
noise = torch.randn_like(x)
x_t = forward_diffuse(x, t, noise)

pred = router(x_t, t) # shape (B, num_clusters)
loss = F.cross_entropy(pred, cluster_idx)
loss.backward()
optimizer.step()

At test-time, we can sample from the entire distribution by ensembling the experts.

# Inside a naive DDM inference loop:
router_pred = router(x_t, t) # shape (B, num_clusters)
router_pred = F.softmax(router_pred, dim=1)

ensemble_pred = torch.zeros_like(x_t)

for i in range(num_clusters):
    model_pred = models[i](x_t, t)
    ensemble_pred += router_pred[:, i] * model_pred

x_t = reverse_step(x_t, t, ensemble_pred)

We can make this more efficient by inferencing experts in parallel and by using a sparse router that only activates a subset of the experts at test-time. In our comparisons, we actually just select the single most relevant expert model per step at test-time.

Acknowledgements

We would like to thank Alex Yu for his guidance throughout the project and his score matching derivation. We would also like to thank Daniel Mendelevitch, Songwei Ge, Dan Kondratyuk, Haiwen Feng, Terrance DeVries, Chung Min Kim, Samarth Sinha, Hang Gao, Justin Kerr and the Luma AI research team for helpful discussions.